Facts

A method to master anything, for example if you want to master social media you need to list all the facts not the opinetad stuff, just facts for example

start from the start

A fact is you are talking to a human

a fact is did people click the video or not

a fact if people left after clicking then there is a wrong

then write down a commone errors you could do in a video

error one click through rate is going down is not the video being bad because they didn’t see the video

etc

now you can go through these fact all over again

You will need to use math logic in these descions for example:

c = clickthrough rate r = video retention if r is down =/ c is bad c does not imply r c ≢ r

by also using the truth table

T T = T F = F T = F F =

example

For example The way my teacher explained the implication and its truth table is as follows.

Suppose I say “If I win the lottery, I will buy you a house!” Logically, this is saying P => Q where P is “I win the lottery” and Q is “I buy you a house”.

Now think about the following: in which cases are you satisfied?

When P is true and Q is true, then I kept my promise and you’re happy. So T => T is T When P is true but Q is false, then I broke my promise. I won the lottery, but didn’t buy you a house. You’re angry, sad, dissapointed. So T => F is F When P is false, I haven’t really made any promises. I never said what I’d do if I did NOT win the lottery. So, if I still buy you a house, you’re definitely going to be happy, but even if I don’t, you won’t be mad because I didn’t win the lottery. Hence, F=>T and F=>F are both T.

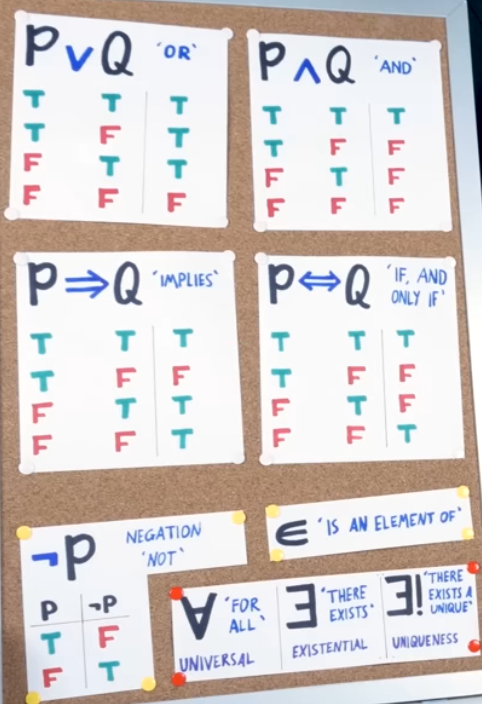
example

Logical Connectives

→ (Implication)
- Meaning: “If-then” (if P, then Q).
- Example: “If it rains (P), then the ground gets wet (Q).”
← (Converse Implication)
- Meaning: “Is implied by” (Q ← P means “Q if P”).
- Example: “The ground is wet (Q) ← it rained (P).”
↔ (Biconditional)
- Meaning: “If and only if” (P ↔ Q means P and Q imply each other).
- Example: “You get a discount ↔ you’re a member.”
∧ (AND)
- Meaning: Both statements are true.
- Example: “Access granted if (password correct ∧ face scan matches).”
∨ (OR)
- Meaning: At least one statement is true.
- Example: “Free shipping if (total ≥ $50 ∨ promo code applied).”
¬ (NOT)
- Meaning: Negation.
- Example: “¬(door open) → alarm triggers.”
⊕ (XOR)
- Meaning: “Exclusive OR” (either P or Q, but not both).
- Example: “A light switch: ON ⊕ OFF.”

Quantifiers

∀ (For All)
- Meaning: Applies to every case.
- Example: “∀ students, attendance is mandatory.”
∃ (There Exists)
- Meaning: At least one case satisfies the condition.
- Example: “∃ a user with admin privileges.”
∃! (There Exists Exactly One)
- Meaning: Uniqueness.
- Example: “∃! prime number that’s even (2).”

Set Theory & Membership

∈ (Element Of)
- Meaning: Belongs to a set.
- Example: “User123 ∈ admins.”
∉ (Not Element Of)
- Meaning: Does not belong to a set.
- Example: “Guest ∉ authorized_users.”
⫫ (Independent Of)
- Meaning: No statistical relationship.
- Example: “Coin flips ⫫ previous outcomes.”

Geometry & Relations

⊥ (Perpendicular/Contradiction)
- Meaning:
  - Geometry: Perpendicular (e.g., line AB ⊥ line CD).
  - Logic: Contradiction (always false).
- Example: “In a proof, assuming P ∧ ¬P leads to ⊥.”
∥ (Parallel To)
- Meaning: Parallel lines/relationships.
- Example: “Railroad tracks ∥ to each other.”

Equality & Approximation